Composite (Laminated) Section Analysis
Equivalent Area Method

For marine design, composite beam analysis is applied when two or more materials are present within a beam's cross section.  Among other things, stiffness differences (materials with differing Young's Modulus values) results in a shift in the location of the cross section's neutral axis.  Discussion in this article is generally confined to a two material cross section.   But in principle, this equivalent area method can be expanded to accommodate more than two materials.

This type of analysis is required quite often for ship and boat design.  For example, in boat hull framing design, you may have a fiberglass hat frame with a layer of carbon fiber on the top surface.  In ship design, you may have a steel hull and an aluminum deckhouse.  This method can also be used by civil engineers who are evaluating stresses in steel reinforced concrete beams.  There are many other scenarios possible. 

The "equivalent area method" is easy to learn, simple to implement, fairly accurate and is adequate for cases involving boat, yacht, ship and barge structural cross sections.  A more direct method or a finite element method can be used if more a sophisticated or more accurate model is required.

With the "equivalent area method" one of the materials is selected to be the base material.  The base material is usually the most dominant material present within the cross section.  The area of the other material is then adjusted laterally to emulate the base material's elastic characteristics.   The height of all materials present must never be modified with this method.  In other words, area transformations for equivalent properties must always be lateral or else this method will not work.

Some other limitations also apply to this method.  This method will work only if the elastic limit, in any of the materials present, is not exceeded.  So, if all working stresses, in all materials, are below their yield strengths, then this method should work fine.  Also differing materials must be adequately connected to each other, so that shearing will not occur at the interfaces.  For instance, aluminum superstructures must be securely bolted or data-clad welded to their steel hulls, and these superstructures must run a substantial length of the hull in order to be effective.  The composite member can also be limited by allowable strains of the resin or the laminate.

Bear in mind when doing composite section analysis, that items closer to the neutral axis can actually experience higher stress than those that are further away.  For example a mahogany beam sitting on top of a steel beam.  The steel beam under the mahogany beam would likely be under higher stress than the mahogany.  For this reason, one should proceed more carefully than one would with isotropic material sections.  Consideration should be given to stresses levels throughout the entire height of a composite beam's cross section.  If the equivalent area calculations are made with a spreadsheet, this checking process can be quick and relatively easy.

Theoretical Derivation of Formulas

Theoretical derivations are straight forward.  For the cross section of the second material present (which is identified as 2), the object is to obtain an equivalent section of base material  (which is identified as 1). 

For equivalence the strain in both the original and transformed members must be the same for a given loading.

For the base material the strain is  Strain1 = Stress1 / E1    and   
for the second material the strain is  Strain2 = Stress2 / E2

Equivalence requires that  Strain1 = Strain2,
therefore Stress1 / E1 = Stress2 / E2; or rearranging we obtain: 

Stress2 / Stress1 = E2 / E1       Formula 1

Also for equivalence, the force carried by the transformed section must equal
the force that is carried by the original second material section.

For the base material the force is  Force1 = Stress1 x A1 and
for the second material the force is Force2 = Stress2 x A2

Since equivalence requires that  Force1 = Force2,
therefore Stress1 x A1 = Stress2 x A2;  solving obtain 
A1 = (Stress2/Stress1) x A2  and rearranging obtain

Stress2 / Stress1 = A1 / A2    Formula 2

Combining the strain (Formula 1) and force (Formula 2) requirements and rearranging obtain the following formulas for equivalent area:

A1 = (E2 / E1) x A2          Formula 3

or   A1 = N2 x A2,            Formula 4

where N2 = E2 / E1           Formula 5       N2 is called the Transformation
                                                                  Factor or Moduli Ratio

Therefore, the equivalent area of base material is equal to the second materials area multiplied by the transformation factor (or moduli ratio which is the second material's modulus divided by the base material's modulus).  Since the height must remain the same for this method to work, the original width of the second material is multiplied by the moduli ratio to obtain an new equivalent width of base material.  So before the transformation the second materials height is h and it's width is w.  After the transformation the second materials height remains at h, and the it's new equivalent width is now N2 x w or (E2/E1) x w.

A formula is now derived to convert the equivalent base material stress (Stess1) calculated in the equivalent section to the actual stress (Stress2) present in the second material's actual section.  This formula is obtained by rearranging Formula 1.  The result is then combined with Formula 5 to incorporate the transformation factor.

Stress2 = Stress1 x (E2 / E1)          Formula 6

Stress2 = Stress1 x N2                 Formula 7

Several sources use Formula 7.  In other words these sources calculate the equivalent section stress in the base material first and then multiply it by the transformation factor. 

When working with spreadsheets there is another more convenient way to get the stress level in Material 2.  This spreadsheet method takes the section modulus of the transformed section and divides it by the transformation factor.  This method skips having to first calculate the stress in the equivalent base material.  This method is derived as follows:

Stress1 = M / SM1, for the equivalent section of base material       Formula 8

Stress2 = M / SM2, for the original second material                       Formula 9

The applied moment is the same for both the equivalent material and second material sections,
so have M = M in Formulas 8 and 9, rearranging obtain:  Stress2 x SM2 = Stress1 x SM1
Rearranging we obtain Stress2 / Stress 1 = SM1 / SM2
Combine the preceding formula with Stress2 / Stress 1 = N2 (rearranged Formula 7)
which is then arranged to give the following formula relating section modulus values:

SM2 = SM1 / N2                         Formula 10 

Rewritten, by combining Formula 10 and Formula 5, and rearranging obtain:

SM2 = SM1 (E1 / E2)                         Formula 10a 

Combining Formula 9 and Formula 10 have the following:

Stress2 = N2 x M / SM1                Formula 11

So the equivalent area section modulus (SM1 of the base material) can be divided by the transformation factor (N2) to obtain the section modulus (SM2) applicable to the original section of second material involved (as per Formula 10). 

Applicability Note 1:  Before proceeding any further, some clarification is required.  The above Formulas 10 and 11 apply to the same point in a cross section.  In these formulas the number 1 represents this point in the transformed cross section consisting of Material 1 and the number 2 represents this same point but this time in Material 2 with a non-transformed (or original) cross section.  This is an important distinction, because the next two formulas, though they can apply to a single point as just mentioned, they are usually applied to completely different points within the cross section.

Substituting SM = I /y into above is Formula 11 and is rewritten as Formula 12 as follows:.

Stress2 = N2 x M x (y2 / I)          Formula 12

Since stress = M / (I / y) by definition, the stress present in Material 1 is:

Stress1 = M x (y1 / I)                   Formula 13

Formulas 12 and 13 are very important and are commonly presented in composite analysis references.  In these formulas, I is the transformed moment of inertia of the cross section.  Note that the same I value is used for both materials present.  However, the y values do change dependant on the material location in the cross section.  For formula 12, the term y2 represents the maximum distance from the neutral axis to the furthest portion of Material 2 in the cross section.  For formula 13, the term y1 represents the maximum distance from the neutral axis to the furthest portion of Material 1 in the cross section.

All the preceding commentary applies to calculating the "available" section modulus.  This available section modulus is the result of materials present and the shape of the cross section.  Though not usually explicitly calculated, a "required" section modulus can be determined through First Principle Analysis.  Normal inputs for required section modulus values are loadings, the geometry present, and allowable stresses.  An applied moment is usually generated and utilized for First Principles Analysis.  Though one is inferred (or implied), a "required" section modulus is not normally calculated.  What usually happens is the applied moment is divided by the "available" section modulus to determine the stresses present.  The allowable stresses are then divided by the stresses present to give the factor of safety present.  If the value is less that one the structure is considered inadequate. 

FS1 = Stress1a / Stress1                Formula 14

FS2 = Stress2a / Stress2                Formula 15

Besides first principles, the marine industry also often has another "required" section modulus.  This "required" section modulus computed through application of classification society rules.  Reference 5 is an example of these types of rules.  These rules have similar inputs to first principles and they also involve loadings, span, allowable material stresses and often other factors to determine a required section modulus.  In Part 4.4.5b of Reference 5, American Bureau of Shipping, the classification society in this case, requires that the required section modulus for the second material be modified as follows (the letter "r" prior to the material numerals indicates "required" section modulus.  The letter "a" after material numerals refers to "allowable" stresses):

SMr2 = SMr1 x (Stress1a / Stress2a)              Formula 16 

Where Stress2a ("u" in the lingo of reference 7) is the verified flexural strength of the alternate laminate and where Stress1a is the verified strength of the basic laminate.  But when Stress1a and Stress2a are not be readily available, it can theoretically be proven that substituting E1 for Stress1 and E2 for Stress2 is equivalent.  The proof goes as follows: Formula 1 can theoretically be modified by inserting the verified (or allowable) flexural stresses instead of the stress levels that are present.  The result is:

(Stress2a / Stress1a) = E2 / E1                         Formula 17   

Formulas 16 is rearranged and then combined with Formula17, the combined result is then rearranged to yield the following:

SMr2 = SMr1 x (E1 / E2)                                  Formula 18 

This formula is very similar to Formula 10a.  The second material modifications for section modulus "available" and section modulus "required" is almost identical.  This is as it should be. 

Note:  The classification society may or may not allow the preceding substitution.  At any rate a documented allowable stress should be available to the designer to verify that the laminate is not overstressed during first principles analysis.  If acceptable stress levels are proven, then the classification society will more likely accept the substitution of Formula 16 with Formula 18 above. 

For composite marine design, Reference 7 has material properties listed for a large number of modern laminates.  References 5 and 8 also has some material properties listed within them.

Cautionary note is added on Page 4, Enclosure A of References 6 and on Page 173 of Reference 7; they state the following:

"Reinforcing fibers of different strengths and different moduli can be limited in the amount of strength that the fibers can develop by the maximum elongation tolerated by the resin and the strain to failure of the surrounding laminate.  Therefore, the strength of the overall laminate should be analyzed, and for marginal safety factor designs or arrangements meeting the minimum of a rule, tests of a sample laminate should be conducted to prove the integrity of the design."

The considerations of this cautionary note are beyond the scope of this short article.  For details and for doing analysis regarding this matter, recommend starting with Reference 7.

Calculative procedure notes:  This article is based on the calculative procedures contained in References 1 through 7.  However, Reference 6 (Enclosure A, Page 4) and Reference 7 (Page 173) modify the required section modulus by also multiplying it by the ratio of material ultimate strengths.  Reference 5 and this article (based on the derivations above) do not incorporate this modification to the required section modulus. 

As just shown, the beauty of this method, is that the moment of inertia of the "transformed" section can be calculated simply as a single material.  Also, the transformation of  materials is easy, in that the width of each non-base material element is simply multiplied by an appropriate transformation factor to get the transformed width for that element.  Additionally, once this transformed moment of inertia is calculated, it is used for all the materials present.  All that needs to be done for an "available" section modulus calculation, is to divide this transformed moment of inertia by the y value for the point under consideration, and if its not the base material divide it by the appropriate transformation factor.  Also if a "required" section modulus is calculated from other sources, all that needs to be done is have it divided by the transformation factor, if it is not of the base material.  For the base of material, the transformation factor is not used.

For an illustration of application with respect to this theoretical derivation, refer to the article entitled "Example of Composite (Laminated) Section Analysis, Equivalent Area Method."

Application of Theory, Characteristics that Apply to Examples that Follow

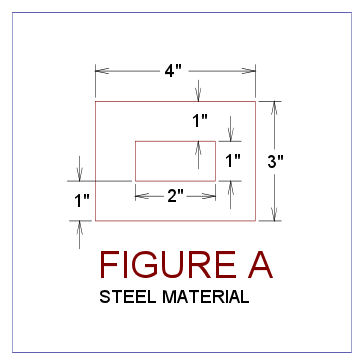
The original (or second) material cross section is for Example One and Two is a steel rectangular tube with 3" overall height with a 4" overall width and a wall thickness of 1" thick.  This means that the tubes interior dimensions is are 1" high x 2" wide.

Three examples follow.  The following material characteristics applies to all the examples. 

Material1, the base material is Aluminum, with E1 = 10 million psi.

Material2, the original (or second) material is Steel, with E2 = 30 million psi.

The Transformation Factor (or Moduli Ratio) is calculated as follows:  N2 = E2 / E1 = 3.00

Example One - Converting a Second Material Element into an Equivalent Area of Base Material Element

An original steel member (or second material cross section) is shown in Figure A.

Converting this original steel cross section to a equivalent aluminum cross section is accomplished as follows:

The interior width of 2" is multiplied by N2 to obtain 6".  The exterior width is the shell thickness of 1" is multiplied by N2 to obtain 3".  No heights have changed.  So the equivalent area overall cross section width is 6" + 3" x 2 = 12".   The height of the upper and lower interior walls remains the same at 1" thick, but the width of the exterior walls are now 3" on each side.  The overall height of 3" remains the same.  This equivalent aluminum section is shown in Figure B below:

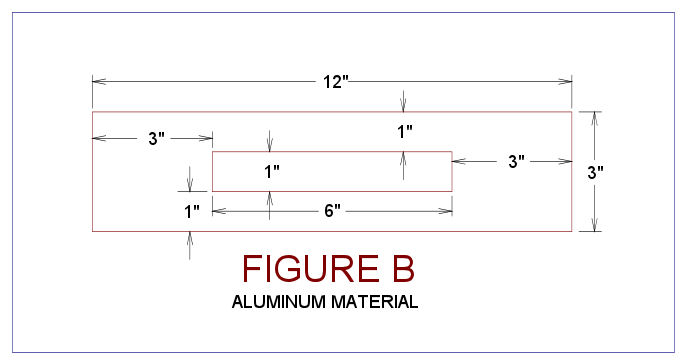
The equivalent moment of inertia for this equivalent area section is computed as follows:

I = 2 x [(1")² x (1"x 6") + (1/12) x 6" x 1"³] + 2 x [(0")² x (3"x 3") + (1/12) x 3" x 3"³] = 2 x (6.5 + 6.75) = 26.5 in⁴

or alternatively calculated for a check as follows:

I = (1/12) x (12" x (3")³ - 6" x (1")³) = 26.5 in⁴

Example Two - Converting the Second Material's Moments of Inertia
to a Representative Material Moment of Inertia of Base Material

A new formula is applied in this section.  In this formula the added material's original moment of inertia is multiplied by the moduli ratio, N2, to obtain the moment of inertia of the equivalent area.  In moment of inertia calculations the heights are cubed, but widths do not change in the equivalent area area section.  So this formula makes sense in this regard.  The following is a proof of this formula.

The moment of inertia of the second material's original section is computed to be I' = (1/12) x (4" x (3")³ - 2" x (1")³) = 8.8333 in⁴

This is then multiplied by the moduli ratio to get the equivalent area moment of inertia as follows:

I = I' x N2 = 8.8333 x 3 = 26.5 in4

This is the same answer as in Example 1, so the hypothesis that the original moment of inertia may be multiplied by the moduli ratio to get the moment of inertia of the equivalent section is now proven.

Example Three - Combining Multiple Sections of Dissimilar Materials

A new cross section is selected for this example, see Figure C below. 

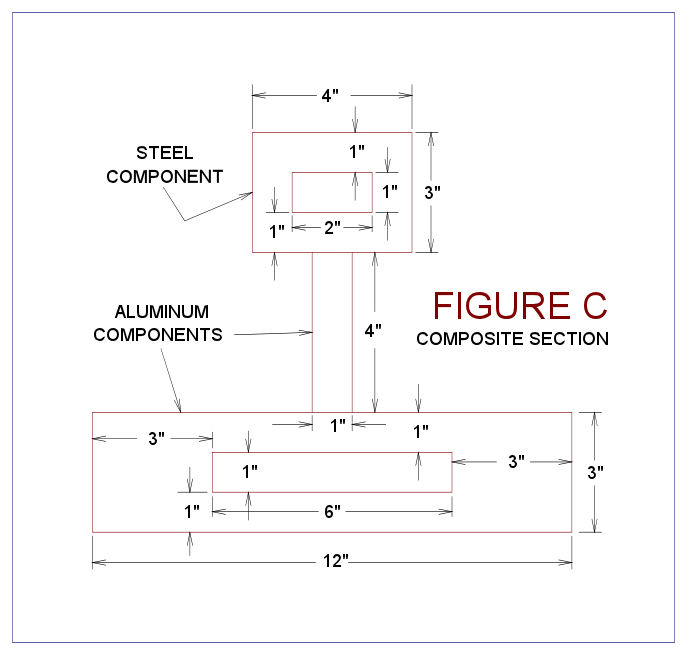
This new cross section is partially composed of elements that are described in Example 1.  More specifically the element on top made of steel as in Example 1; the middle element is a new 1" x 4" aluminum flat bar, which is standing vertically; and the bottom is aluminum element as shown in Figure B of Example 1.  Figure C requires transformation; this transformation is shown below.  Note that the upper steel element was transformed as per Example 1.

The transformed sections moment of inertia for this new section is calculated as
I = (4"/2 + 1.5")² x (12" x 3" - 1" x 6") + 2 x 26.5 + (1/12) x 1" x (4")³ = 3.5² x 30 + 53 + 5.333 = 425.833 in⁴

The largest stress in the aluminum will be at the bottom of the member, the section modulus corresponding to this stress is computed as follows:
SM1 = (I / y) = 425.833 / (4"/2 + 3") = 85.167 in³
Stress1 = M / SM1

The largest stress in the steel will be at the top of the member, and the section modulus corresponding to this stress is computed as follows:
SM2 = (I / y) x [1 / (E2/E1)] = [425.833 / (4"/2 + 3")] x (1/3) = 28.389 in³
Stress2 = M / SM2

Since M is the same, the steel will be under a larger stress because it's section modulus is smaller.  But the steel also has a larger allowable stress which helps offsets it's greater stress levels.

The preceding sample section was selected solely for conceptual teaching purposes.  Due to inevitable minor deformities from the construction process, this section may twist some when it is subjected to flexural loads.  Without additional checks, it is not recommended that a section looking like this actually be used in practice.  Fortuitously most boat, ship and barge structural shapes less susceptible to twisting action.

Another Example - Douglas Fir and Fiberglass Laminate

This example cross consists of a 2" x 4" piece of Douglas Fir plywood that is standing upright on a 1/4" thick 14" fiberglass plating element that is laying flat. The fiberglass is standard laminate as per ABS requirements.  This example is presented on Composite Beam Equivalent Area Method Example.

Summary

The cross section properties of a two material beam can be easily determined through the "Equivalent Area" method.   This method transforms one material's cross sectional area to facilitate the other material that is present.  After transformations are made the whole cross section can be evaluated in a conventional manner, that is as one homogenous material.

The transformation is accomplished by multiplying area sections by a "transformation factor."  The transformation is always lateral and not vertical.  The transformation factor is the modulus of elasticity of the material being transformed divided by the modulus of elasticity of the base material of the cross section.  Portions of the beam that are made out of the base material are not transformed.

The transformed section is evaluated just like a isotropic material section.  With the exception, that an original material moments of inertia, if they are used, are also multiplied by transformation factor.  This refers to the moments of inertia about the neutral axis of original material.  This may occur if the original material's area properties are pulled off a table (AISC table for example) or computed by hand (like for a triangular shape).  This would not apply, if the original material was a rectangle, and it's moment of inertia about it's own neutral axis is calculated based on the transformed area of the element involved.

Section modulus values of base material elements require no modifications.  But section modulus values of non-base material must be divided by the transformation factor to give a section modulus that applies to the non-base material.  Alternatively, the non-base material stress can be calculated as if it is base material, and then modified by multiplying the base material stress by the transformation factor, which will yield the stress present in the non-base material.

Primary References

Composite beam analysis is described described on the web in several places.  Some of these places are listed as follows:

1. EN358 Ship Structures, Course Notes, U. S. Naval Academy, Annapolis, MD.  This is a large document, see the section entitled "Composite Beam Approach (Dissimilar Materials)."

2. High Strength Composites Course, University of Utah.  The section entitled "Composite (laminated) beam" applies in this discussion.

3. Mechanics eBook: Composite Beams, University of Oklahoma.  See last section entitled "Alternative Method - Equivalent Area."

4. Rules for Building and Classing Reinforced Plastic Vessels, 1978, American Bureau of Shipping.

5. NVIC 8-87, Notes on Design, Construction, Inspection and Repair of Fiber Reinforced Plastic (FRP) Vessels, USCG, Washington, D. C..  This is a very large document, for pertinent details go to Enclosure 1, Part B Determining Section Modulus and Moment of Inertia.

6. Buckling of Transversely Framed Panels, Chapter 3, Marine Composites, Eric Greene Associates, Annapolis, MD.  See pages 172 and 173 for an example of composite section calculations.

7. Rules for Materials and Welding, Part 2 Aluminum & Fiber Reinforced Plastic (FRP) (Chapters 5-6), 2006 American Bureau of Shipping.

8. Fiberglass Boat Design and Construction,
   by Robert J. Scott, 1996 Second Edition, Society of Naval Architects & Marine Engineers.

9. Fiberglass Boatbuilding for Amateurs,
   by Ken Hankinson, 1982, Glen-L Marine Designs, Bellflower, California.

Applications: The concepts described in this article are utilized in the following templates:

• Equivalent Area Method, Composite (Laminated) Section Analysis, U. S. A. Units                     

• Equivalent Area Method, Composite (Laminated) Section Analysis, Metric Units

Though not directly related to composite analysis, learning the parallel axis theorem is helpful for structural analysis.  This subject is covered in an article that is entitled "Parallel Axis Theorem."